Linear Discriminant Analysis ( LDA) with Scikit

November 14, 2017May 16, 2021 / RP / 1 Comment

Linear Discriminant Analysis (LDA) is similar to Principal Component Analysis (PCA) in reducing the dimensionality. However, there are certain nuances with LDA that we should be aware of-

LDA is supervised (needs categorical dependent variable) to provide the best linear combination of original variables while providing the maximum separation among the different groups. On the other hand, PCA is unsupervised
LDA can be used for classification also, whereas PCA is generally used for unsupervised learning
LDA doesn’t need the numbers of discriminant to be passed on ahead of time. Generally speaking the number of discriminant will be lower of the number of variables or number of categories-1.
LDA is more robust and can be conducted without even standardizing or normalizing the variables in certain cases
LDA is preferred for bigger data sets and machine learning

Let the action begin now-

lda1 LDA2 LDA3 LDA4 LDA5

Cheers!

Principal Component Analysis ( PCA) using Scikit

November 14, 2017May 16, 2021 / RP / 2 Comments

Principal Component Analysis ( PCA) is generally used as an unsupervised algorithm for reducing the data dimensions to address Curse of Dimensionality, detecting outliers, removing noise, speech recognition and other such areas.

The underlying algorithm in PCA is generally a linear algebra technique called Singular Value Decomposition (SVD). PCAs take the original data and create orthogonal components (uncorrelated components) that capture the information contained in the original data however with significantly less number of components.

Either the components themselves or key loading of the components can be plugged in any further modeling work, rather than the original data to minimize information redundancy and noise.

There are three main ways to select the right number of components-

Number of components should explain at least 80% of the original data variance or information [Preferred One]
Eigen value of each PCA component should be more than or equal to 1. This means that they should express at least one variable worth of information
Elbow or Scree method- look for the elbow in the percentage of variance explained by each components and select the components where an elbow or kink is visible.

You can use any one of the above or combination of the above to select the right number of components. It is very critical to standardize or normalize data before conducting PCA.

In the below case study we will use the first criterion shown above, i.e. 80% or more of the original data variance should be explained by the selected number of components.

PCA1 PCA2 PCA3 PCA4 PCA5 PCA6

Decision Tree using Python Scikit

November 4, 2017May 16, 2021 / RP / 1 Comment

If you are not familiar with Decision Trees, please read this article first.

First let’s look at a very simple example on the Iris data-

Decision Tree in Python

Now let’s look at slightly more complex data-

Let’s first build a logistic regression model in Python using machine learning library Scikit. Please read here about the dataset and dummy coding.

clf1 clf2 clf3 clf4 clf5 clf6 clf7

dt1 dt2 dt3 dt4

Cheers!

Logistic Regression using Scikit Python

November 4, 2017May 16, 2021 / RP / 1 Comment

If you are not familiar with logistics regression, please read this article first. Moreover, if you are not familiar with the sklearn machine learning model building process, please read this article also.

Assuming you are now familiar, this is how you can build a logistic regression model in Python using machine learning library Scikit. Please read here about the dataset and dummy coding.

clf1 clf2 clf3 clf4 clf5 clf6 clf7

clf8 clf9 clf10

Cheers!

Categorical Variables Dummy Coding

November 4, 2017May 16, 2021 / RP / 3 Comments

Converting categorical variables into numerical dummy coded variable is generally a requirement in machine learning libraries such as Scikit as they mostly work on numpy arrays.

In this blog, let’s look at how we can convert bunch of categorical variables into numerical dummy coded variables using four different methods-

Scikit learn preprocessing LabelEncoder
Pandas getdummies
Looping
Mapping

We will work with a dataset from IBM Watson blog as this has plenty of categorical variables. You can find the data here. In this data, we are trying to build a model to predict “churn”, which has two levels “Yes” and “No”.

We will convert the dependent variable using Scikit LabelEncoder and the independent categorical variables using Pandas getdummies. Please note that LabelEncoder will not necessarily create additional columns, whereas the getdummies will create additional columns in the data. We will see that in the below example-

clf1 clf2 clf3 clf4 clf5 clf6 clf7

Here are few other ways to dummy coding-

dummy_coding1 dummy_coding2 dummy_coding3

Here is an excellent Kaggle Kernel for detailed feature engineering.

Cheers!

Hierarchical Clustering with Python

November 4, 2017May 16, 2021 / RP / 2 Comments

As highlighted in the article, clustering and segmentation play an instrumental role in Data Science. In this blog, we will show you how to build a Hierarchical Clustering with Python.

For this purpose, we will work with a R dataset called “Cheese”. Please install package called “Bayesm” in R and export this data set in csv format to be imported in Python. More on this dataset can be found here.

Let’s begin with the clustering in Python then. hclust1 hclust2 hclust3 hclust4 hclust5 hclust6 hclust7

hclust8

Cheers!

KMeans Clustering: Core Concepts, Assumptions, and Key Equations

November 4, 2017August 10, 2025 / RP / 3 Comments

Overview:
KMeans is an unsupervised machine learning algorithm used to partition data into a specified number of clusters (k). Each cluster is defined by its centroid, and the algorithm aims to minimize the distance between data points and their assigned cluster centroids.

Core Concepts:

Clusters and Centroids:
- A cluster is a group of data points that are similar to each other.
- The centroid is the mean position of all the points in a cluster.
Assignment and Update Steps:
- Assignment: Each data point is assigned to the nearest centroid.
- Update: The centroids are recalculated as the mean of all points assigned to each cluster.
Iterative Optimization:
- The assignment and update steps are repeated until the centroids no longer change significantly or a maximum number of iterations is reached.

Assumptions:

The number of clusters (k) is known and fixed in advance.
Clusters are roughly spherical and equally sized.
Data points are closer to their own cluster centroid than to others.
The algorithm is sensitive to the initial placement of centroids.

Key Equations:

Distance Calculation:
- The most common distance metric is Euclidean distance.
- For a data point x and centroid c:
  Distance = sqrt( (x1 – c1)^2 + (x2 – c2)^2 + … + (xn – cn)^2 )
Centroid Update:
- For each cluster, the new centroid is the mean of all points assigned to that cluster.
- Centroid for cluster j:
  cj = (1 / Nj) * sum(xi)
  where Nj is the number of points in cluster j, and xi are the points in cluster j.
Objective Function (Inertia):
- KMeans minimizes the sum of squared distances (inertia) between each point and its assigned centroid.
- Inertia = sum over all clusters j [ sum over all points i in cluster j (distance(xi, cj))^2 ]

Algorithm Steps:

Choose k initial centroids (randomly or using a method like k-means++).
Assign each data point to the nearest centroid.
Recalculate centroids as the mean of assigned points.
Repeat steps 2 and 3 until centroids stabilize.

Limitations:

Sensitive to outliers and noise.
May converge to a local minimum (results can vary with different initializations).
Not suitable for clusters with non-spherical shapes or very different sizes.

Applications:

Market segmentation
Image compression
Document clustering
Anomaly detection

# Simple KMeans Clustering Example
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score

# Generate synthetic data
X, y_true = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=42)

# Elbow method to find optimal k
inertia = []
k_range = range(1, 11)
for k in k_range:
    kmeans = KMeans(n_clusters=k, random_state=42)
    kmeans.fit(X)
    inertia.append(kmeans.inertia_)
plt.figure(figsize=(6,4))
plt.plot(k_range, inertia, 'bo-')
plt.axvline(x=4, color='red', linestyle='--', label='Optimal k=4')
plt.xlabel('Number of clusters (k)')
plt.ylabel('Inertia')
plt.title('Elbow Method for Optimal k')
plt.legend()
plt.grid(True)
plt.show()

# Fit KMeans with optimal k (choose visually, e.g., k=4)
k_opt = 4
kmeans = KMeans(n_clusters=k_opt, random_state=42)
labels = kmeans.fit_predict(X)

# Plot clusters
plt.figure(figsize=(7,5))
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', s=50)
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], c='red', s=200, alpha=0.75, marker='X', label='Centers')
plt.title(f'KMeans Clustering (k={k_opt})')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.show()

# Silhouette score
score = silhouette_score(X, labels)
print(f'Silhouette Score (k={k_opt}): {score:.3f}')

Silhouette Score (k=4): 0.876

# KMeans Clustering on Iris Dataset
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
import pandas as pd

# Load Iris data
iris = load_iris()
X = iris.data

# Elbow method to find optimal k
inertia = []
k_range = range(1, 11)
for k in k_range:
    kmeans = KMeans(n_clusters=k, random_state=42)
    kmeans.fit(X)
    inertia.append(kmeans.inertia_)
k_opt = 3  # Set optimal k explicitly for Iris data
plt.figure(figsize=(6,4))
plt.plot(k_range, inertia, 'bo-')
plt.axvline(x=k_opt, color='red', linestyle='--', label='Optimal k=3')
plt.xlabel('Number of clusters (k)')
plt.ylabel('Inertia')
plt.title('Elbow Method for Optimal k (Iris)')
plt.legend()
plt.grid(True)
plt.show()

# Fit KMeans with optimal k (choose visually, e.g., k=3)
kmeans = KMeans(n_clusters=k_opt, random_state=42)
labels = kmeans.fit_predict(X)

# Plot clusters (using first two features for visualization)
plt.figure(figsize=(7,5))
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', s=50)
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], c='red', s=200, alpha=0.75, marker='X', label='Centers')
plt.title(f'Iris KMeans Clustering (k={k_opt})')
plt.xlabel(iris.feature_names[0])
plt.ylabel(iris.feature_names[1])
plt.legend()
plt.show()

# Plot clusters (using petal length and petal width for visualization)
plt.figure(figsize=(7,5))
plt.scatter(X[:, 2], X[:, 3], c=labels, cmap='viridis', s=50)
plt.scatter(kmeans.cluster_centers_[:, 2], kmeans.cluster_centers_[:, 3], c='red', s=200, alpha=0.75, marker='X', label='Centers')
plt.title(f'Iris KMeans Clustering (k={k_opt}) - Petal Length vs Petal Width')
plt.xlabel(iris.feature_names[2])
plt.ylabel(iris.feature_names[3])
plt.legend()
plt.show()

# Silhouette score
score = silhouette_score(X, labels)
print(f'Silhouette Score (k={k_opt}): {score:.3f}')

# Number of observations in each cluster
unique, counts = np.unique(labels, return_counts=True)
for i, count in zip(unique, counts):
    print(f"Cluster {i}: {count} data points")

# Descriptive summary of each cluster (mean feature values)
df = pd.DataFrame(X, columns=iris.feature_names)
df['cluster'] = labels
print("\nCluster feature means:")
print(df.groupby('cluster').mean())

Cheers!

Python Machine Learning Linear Regression with Scikit- learn

October 31, 2017May 16, 2021 / RP / 3 Comments

What is a “Linear Regression”-

Linear regression is one of the most powerful and yet very simple machine learning algorithm. Linear regression is used for cases where the relationship between the dependent and one or more of the independent variables is supposed to be linearly correlated in the following fashion-

Y = b0 + b1*X1 + b2*X2 + b3*X3 + …..

Here Y is the dependent variable and X1, X2, X3 etc are independent variables. The purpose of building a linear regression model is to estimate the coefficients b0, b1, b2 et cetera that provides the least error rate in the prediction. More on the error will be discussed later in this article.

In the above equation, b0 is the intercept, b1 is the coefficient for variable X1, b2 is the coefficient for the variable X2 and so on…

What is a “Simple Linear Regression” and “ Multiple Linear Regression”?

When we have only one independent variable, resulting regression is called a “Simple Linear Regression” when we have 2 or more independent variables the resulting regression is called “Multiple Linear Regression”

What are the requirements for the dependent and independent variables in the regression analysis?

The dependent variable in linear regression is generally Numerical and Continuous such as sales in dollars, gdp, unemployment rate, pollution level, amount of rainfall etc. On the other hand, the independent variables can be either numeric or categorical. However, please note that the categorical variables will need to be dummy coded before we can use these variables for building a regression model in the sklearn library of Python.

What are some of the real world usage of linear regression?

As we discussed earlier, this is one of the most commonly used algorithm in ML. Some of the use cases are listed below-

Example 1-

Predict sales amount of a car company as a function of the # of models, new models, price, discount,GDP, interest rate, unemployment rate, competitive prices etc.

Example 2-

Predict weight gain/loss of a person as a function of calories intake, junk food, genetics, exercise time and intensity, sleep, festival time, diet plans, medicines etc.

Example 3-

Predict house prices as a function of sqft, # of rooms, interest rate, parking, pollution level, distance from city center, population mix etc.

Example 4-

Predict GDP growth rate as a function of inflation, unemployment rate, investment, new business, weather pattern, resources, population

How do we evaluate linear regression model’s performance?

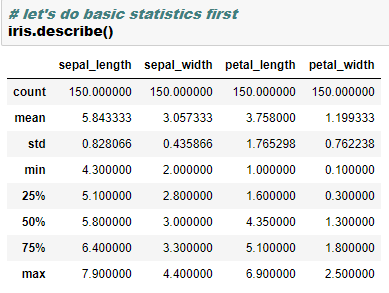
There are many metrics that can be used to evaluate a linear regression model’s performance and choose the best model. Some of the most commonly used metrics are-

Mean Square Error (MSE)- This is an error and lower the amount the better it is. It is defined using the below formula

Mean Absolute Percent Error (MAPE)- This is an error and lower the amount the better it is. It is defined using the below formula

R Square– This is called coefficient of determination and provides a gauge of model’s explaining power. For example, for a linear regression model with a RSquare of 0.70 or 70% would imply that 70% of the variation in the dependent variable can be explained by the model that has been built.

How do we build a linear regression model in Python?

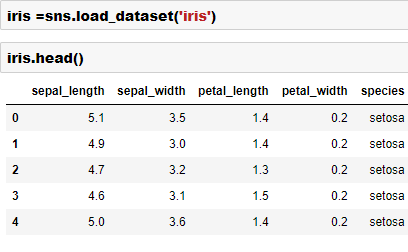
In this exercise, we will build a linear regression model on Boston housing data set which is an inbuilt data in the scikit-learn library of Python. However, before we go down the path of building a model, let’s talk about some of the basic steps in any machine learning model in Python

In most cases, any of the machine learning algorithm in sklearn library will follow the following steps-

Split original data into features and label. In other words, create dependent variable and set of independent variables in two different arrays separately. Please note this requirement exists only for the supervised learning ( where a dependent variable is present). For unsupervised learning, we don’t have a dependent variable and hence there is no need to split the data into features and label
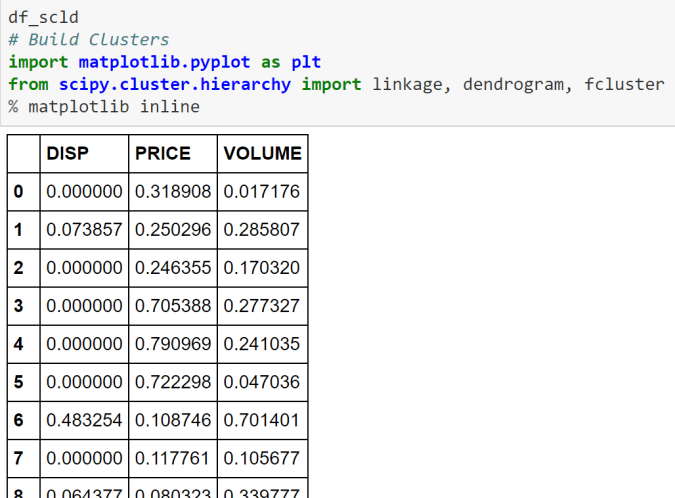
Scale or Normalize the features and label data. Please note that this is not a necessity for all algorithms and/or datasets. Also we are assuming that all the data cleaning and feature engineering such as missing value treatment, outlier treatment, bogus values fixes and dummy coding of the categorical variables have been done before doing this step
Create training and test data sets from the original data. Training data set will be used for training the model whereas the test data set will be used for validating the accuracy or the prediction power of the model on a new dataset. We would need to split both the features and labels into the training and the test split.
Create an instance of the model object that will be used for the modelling exercise. This process is called “Instantiation”. In simpler words, during this process we are loading the model package necessary to build a model.
“Fit” the model instance on the training data. During this step, the model is leveraging both the features and the label information provided in the training data to connect the features to label. Please note that we are going with all the default option during fitting of the model. As you get more expertise you may want to play with some parameter optimization, however we are just going with the defaults for now.
“Predict” using the model instance on test data. During this step, the model is only using the features information to predict the label.
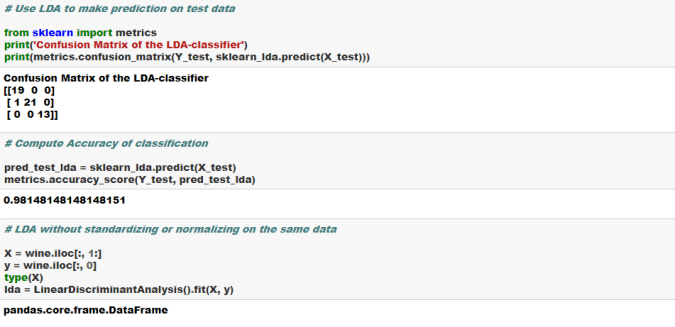
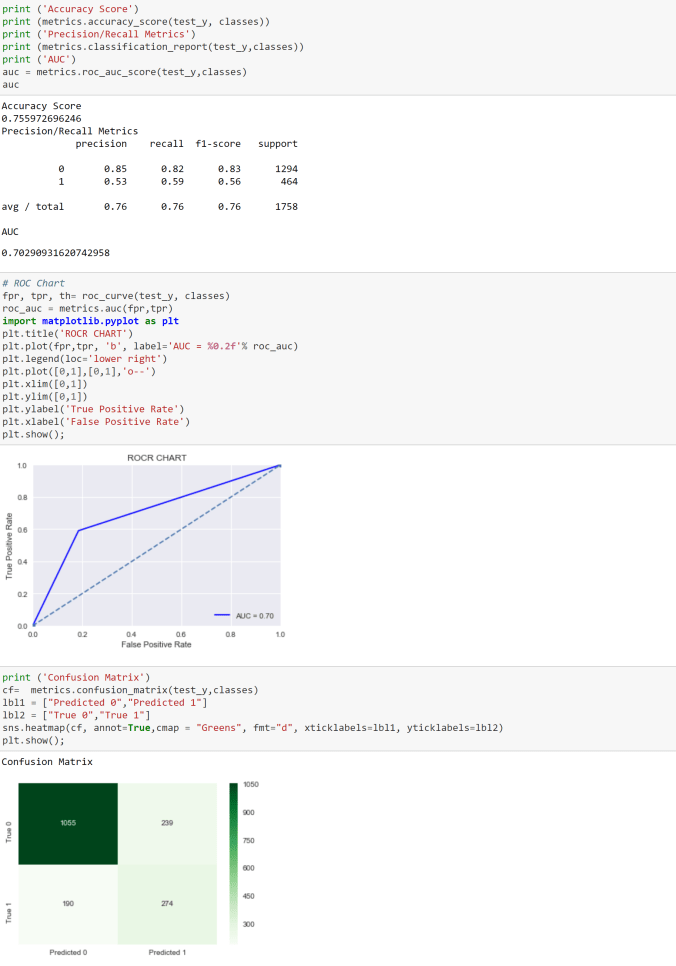
Based on the predictions generated on the test data, we generate key performance indicators of model performance. This generally includes metrics such as Precision, Recall F score, Confusion Matrix, Accuracy, Mean Square Error (MSE), Root Mean Square Error (RMSE), Mean Absolute Error (MAE), Area Under the Curve (AUC), Mean Absolute Percentage error (MAPE) etc.
Once the model performance is evaluated and its deemed to be satisfactory for the purpose of the business uses, we implement the model for new unseen data

So let’s get started with building this model-

import the necessary packages including the train_test_split package which will be used for splitting the data into the training and test samples

Import interactive shell magic command which will help us print many statements on the same line

Import the Boston Housing dataset from sklearn library. Python has many such inbuilt datasets for various purposes. Most of the data sets in such libraries are stored as dictionary format.

Find out more about this data set by typing the below command
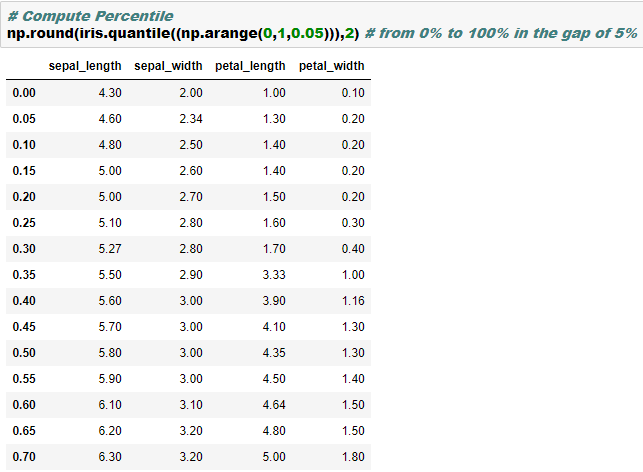
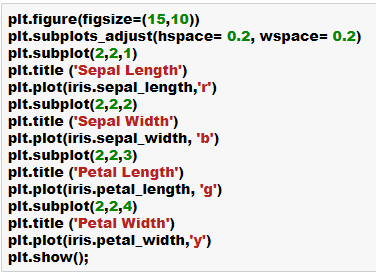
Let’s do some more exploratory analysis such as- printing the features, the label shape of the data etc.

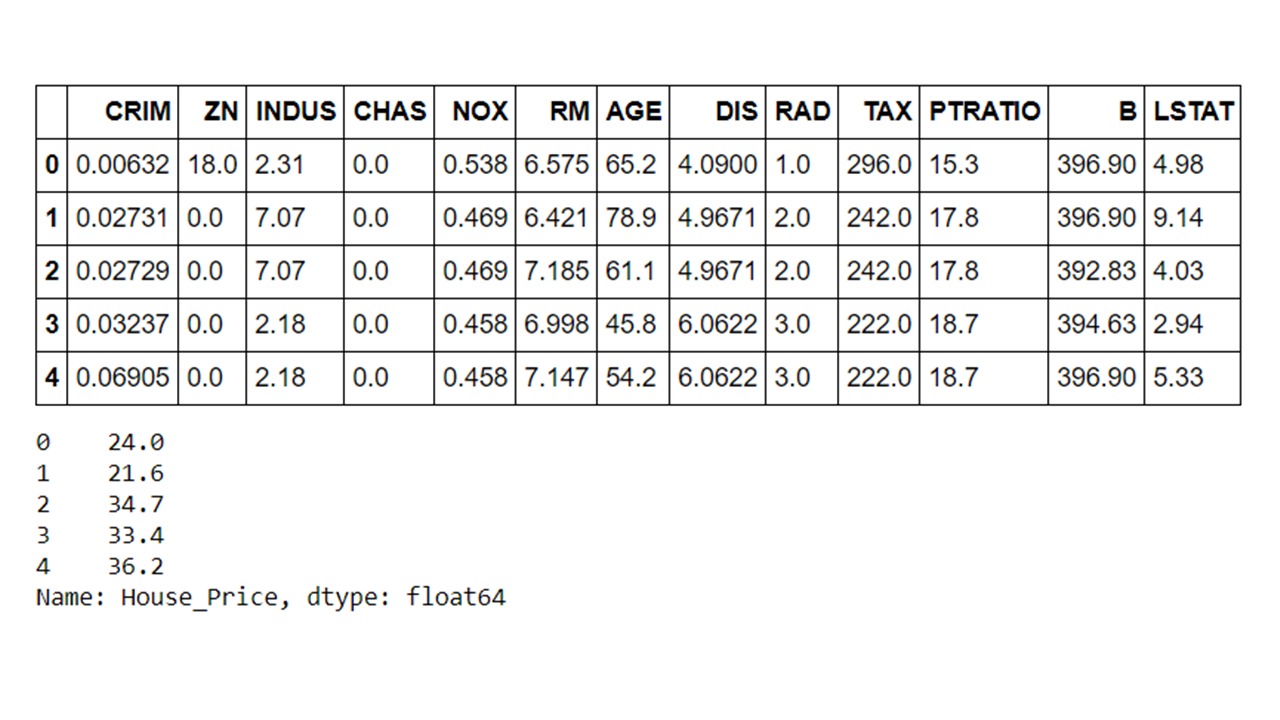
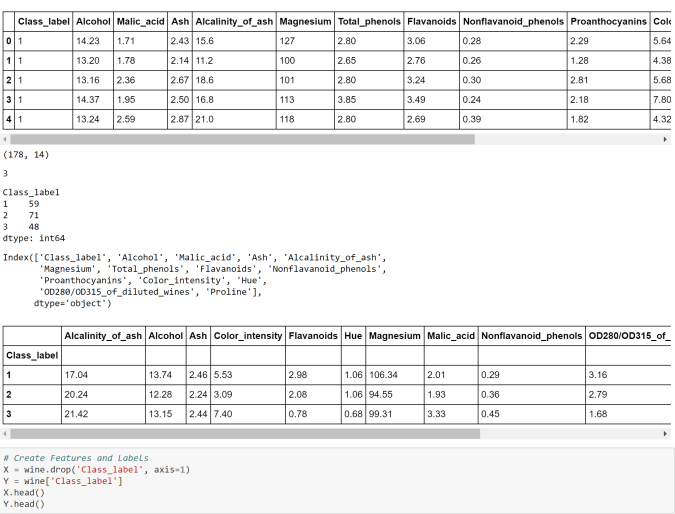
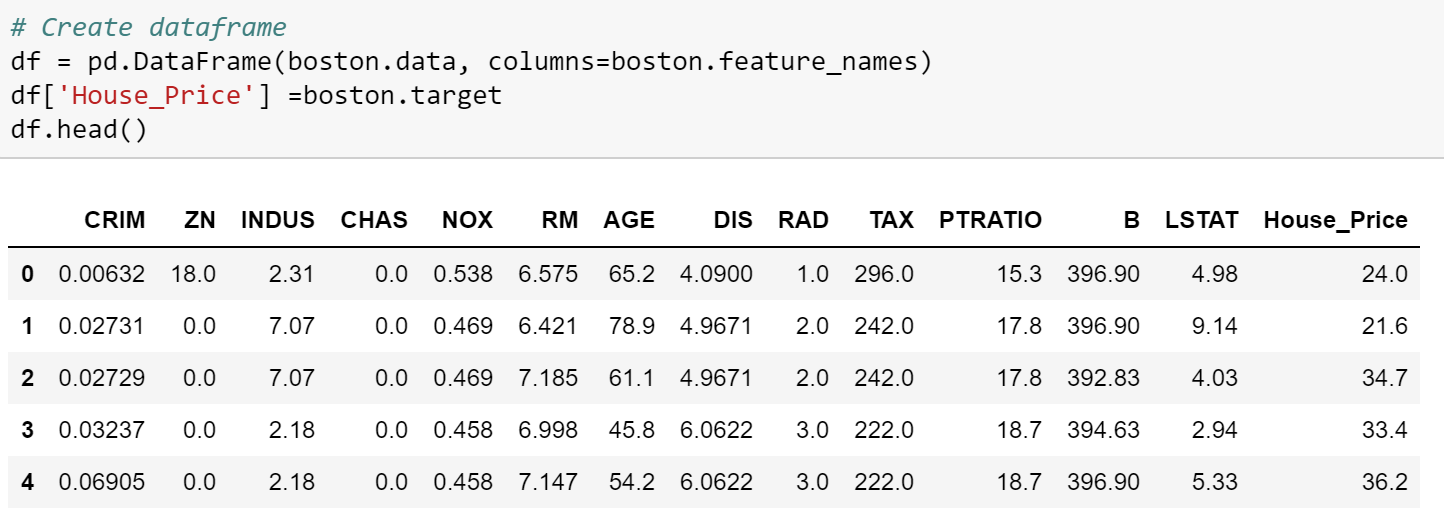
Convert the original array data into a dataframe and append the column names.
Add a new variable in the dataframe for the target ( or label) variable

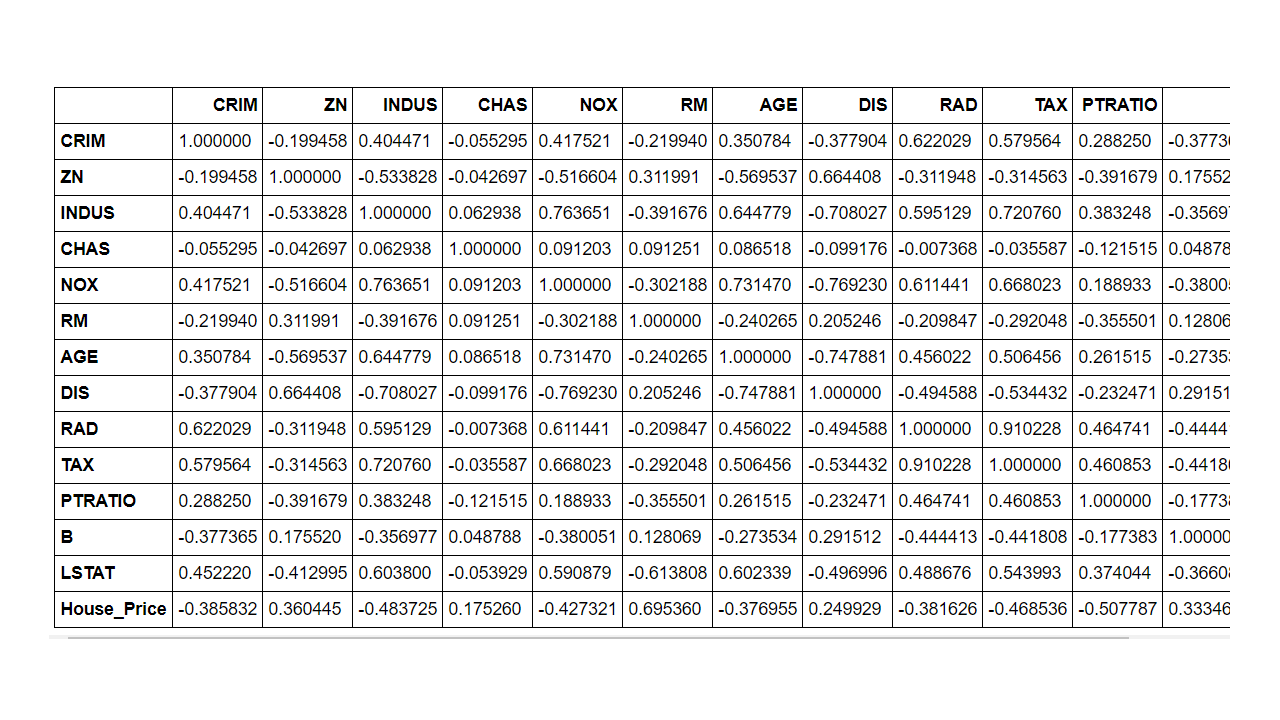
Since we are building a linear regression model it may be helpful to generate the correlation matrix and then the correlation heatmap using the seaborn library

Create features and labels using Pandas ‘.drop() ‘ method to drop certain variables. In this case we are dropping the house price as this is the label.

Split the data into the training and test datasets

Instantiate– import the model object and create an instance of the model

Fit – Fit the model instant on the training data using ‘ .fit() ‘ method. Note that we are passing on both the features and label here

Predict– Predict using the model instant and training done on the training data using ‘ .predict() ‘ method. Please note that here we are only passing on the features and having the model predict the values of the label.

We can find out many important things such as the coefficients of the parameters using the fitted object methods. In the below case, we are getting the coefficient values for all the feature parameters in the model.

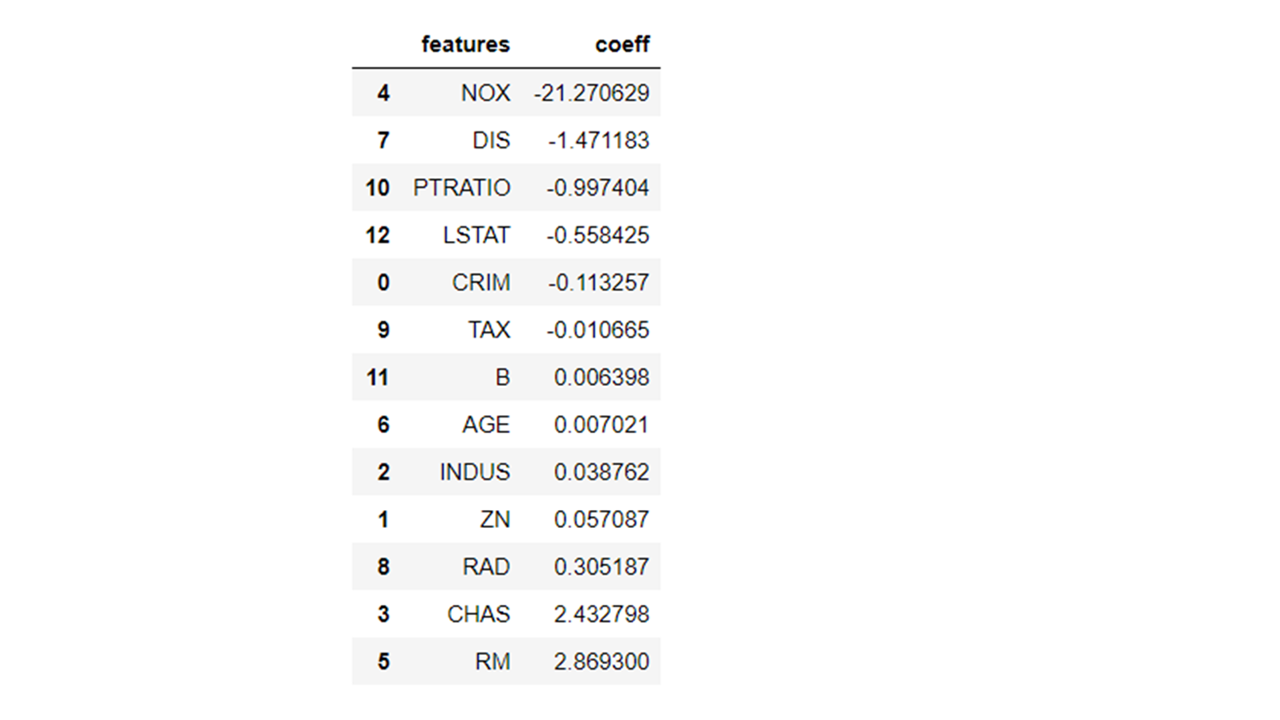
We can plot the feature importance in a bar chart format as well using the ‘.plot’ method of the Pandas dataframe. Please note that we can also specify the figure size and the X and Y variables in the plot method under the different parameters possible

Let’s now generate some of the model performance metrics such as R2, MSE and MAE. All of these model performance metrics can be generated using the scikit-learn inbuilt packages such as ‘metrics’.

In the last step we are appending the predicted house prices into the original data and computing the error in estimation for the test data.

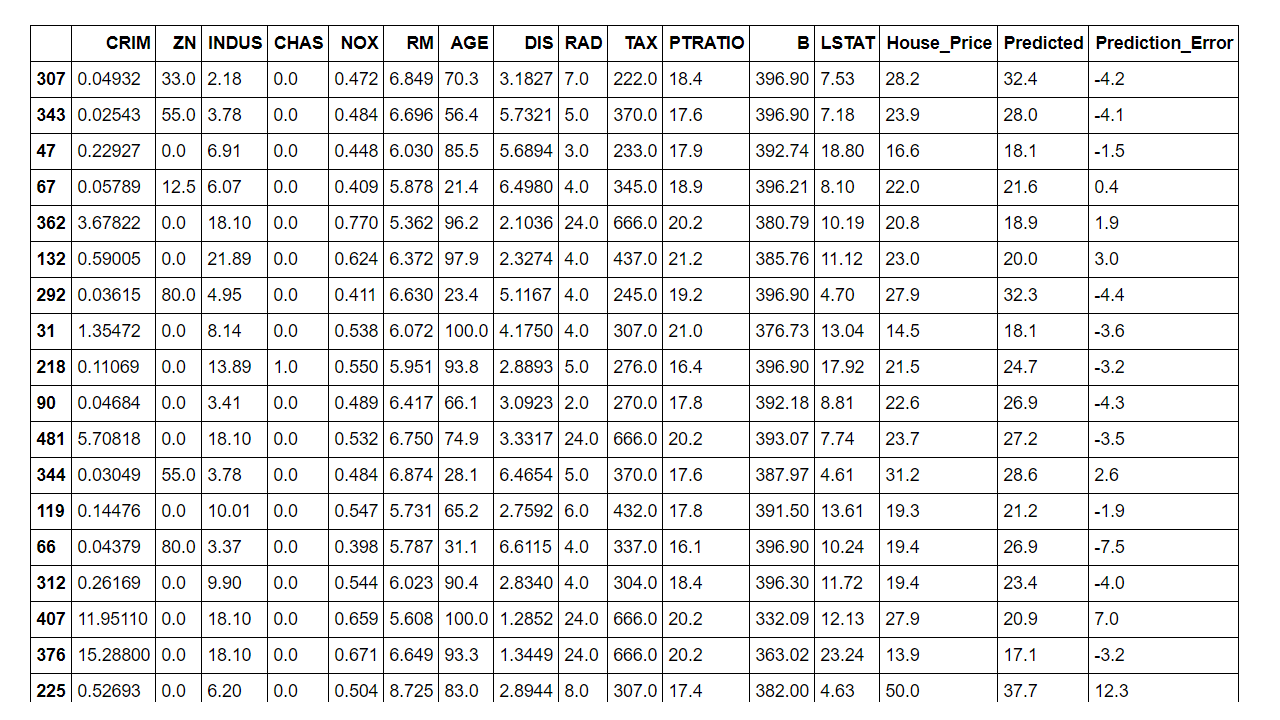
As you can see from the above metrics that overall this plain vanilla regression model is doing a decent job. However, it can be significantly improved upon by either doing feature engineering such as binning, multicollinearity and heteroscedasticity fixes etc. or by leveraging more robust techniques such as Elastic Net, Ridge Regression or SGD Regression, Non Linear models.

—

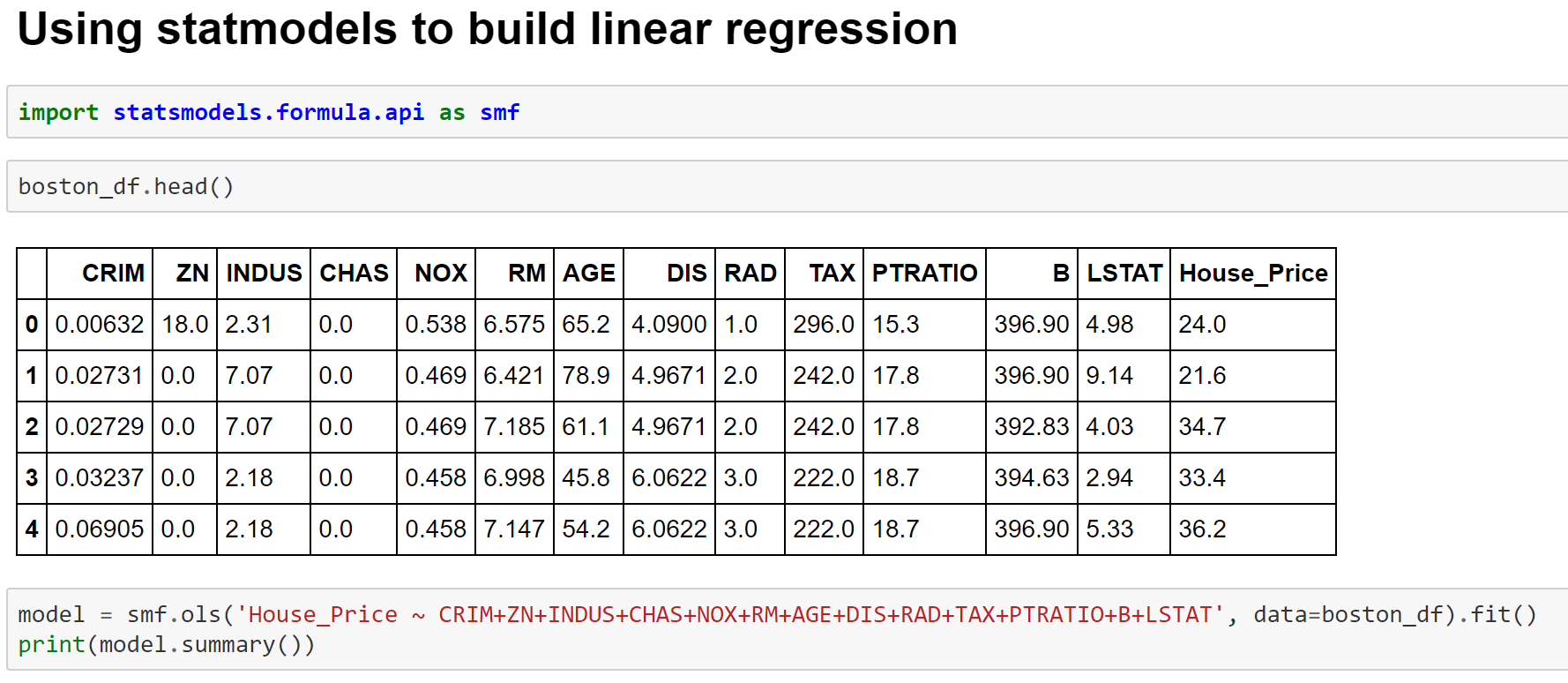
Image 9- Fitting Linear Regression Model using Statmodels

Image 10- OLS Regression Output

Image 11- Fitting Linear Regression Model with Significant Variables

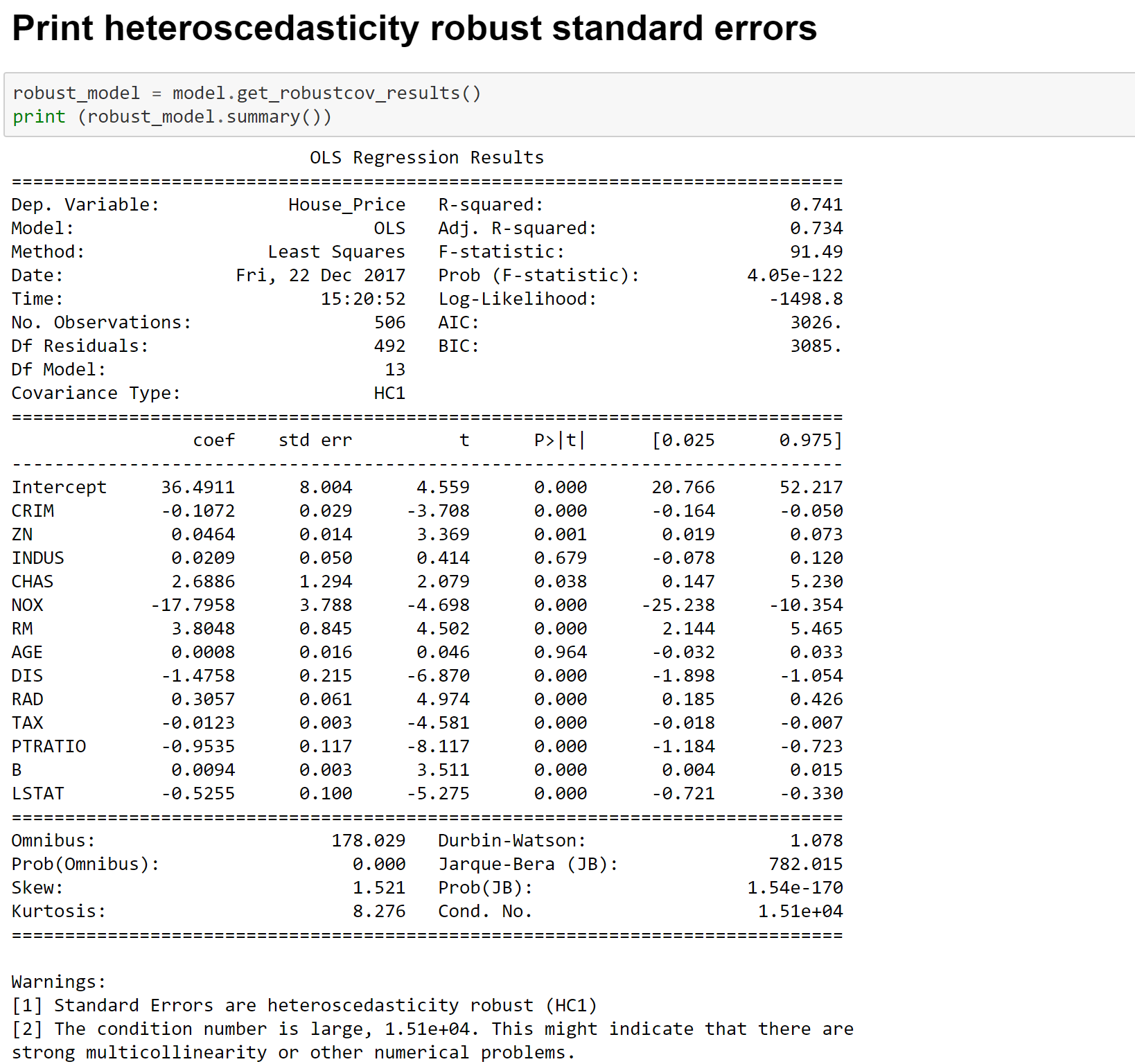
Image 12- Heteroscedasticity Consistent Linear Regression Estimates

More details on the metrics can be found at the below links-

Wiki

Here is a blog with excellent explanation of all metrics

Cheers!

Data Standardization or Normalization

October 27, 2017May 16, 2021 / RP / 1 Comment

Data standardization or normalization plays a critical role in most of the statistical analysis and modeling. Let’s spend sometime to talk about the difference between the standardization and normalization first.

Standardization is when a variable is made to follow the standard normal distribution ( mean =0 and standard deviation = 1). On the other hand, normalization is when a variable is fitted within a certain range ( generally between 0 and 1). Here are more details of the above.

Let’s now talk about why we need to do the standardization or normalization before many statistical analysis?

In a multivariate analysis when variables have widely different scales, variable(s) with higher range may overshadow the other variables in analysis. For example, let’s say variable X has a range of 0-1000 and variable Y has a range of 0-10. In all likelihood, variable X will outweigh variable Y due to it’s higher range. However, if we standardize or normalize the variable, then we can overcome this issue.
Any algorithms which are based on distance computations such as clustering, k nearest neigbour ( KNN), principal component ( PCA) will be greatly affected if you don’t normalize the data
Neural networks and deep learning networks also need the variables to be normalized for converging faster and giving more accurate results
Multivariate models may become more stable and the coefficients more reliable if you normalize the data
It provides immunity from the problem of outliers

Let’s look at a Python example on how we can normalize data-

scaling1 scaling2 scaling3 scaling4 scaling5 scaling6